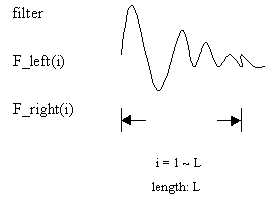
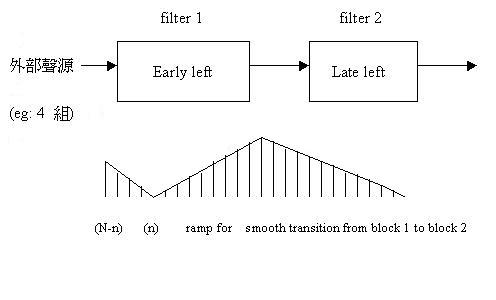
Fourier Transform, Discrete Fourier Transform:  Introduction

e^it = cos(t) + i sin(t)

Continuous

For a continuous function of one variable f(t), the Fourier Transform F(f) will be defined as:

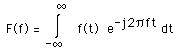
and the inverse transform as

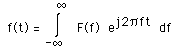
where j is the square root of -1 and e denotes the natural exponent

Discrete

Consider a complex series x(k) with N samples of the form

where x is a complex number

Further, assume that that the series outside the range 0, N-1 is extended N-periodic, that is, x_k = x_k+N for all k. The FT of this series will be denoted X(k), it will also have N samples. The forward transform will be defined as

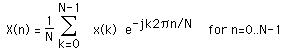
The inverse transform will be defined as

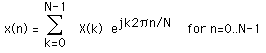
Convolution:  Convolution in time domain equals multiplication in frequency domain.

The behavior of a linear, time-invariant discrete-time system with input signalx[n] and output signal y[n] is described by the convolution sum

For longer sequences, convolution may pose a problem of processing time; it is often preferred to perform the operation in the frequency domain: if X, Y and Z are the Fourier transforms of x, y and z, respectively, then:

Normally one uses a fast Fourier transform (FFT), so that the transformation becomes

For the FFT, sequences x and y are padded with zeros to a length of a power of 2 of at least M + N - 1 samples.

DEMO:   http://www.srslabs.com/Demonstrations.asp