Computer Organization and Structure
Homework #3
Due: 2003/11/11
1.
Convert 512ten, -1,023ten,
and -4,000,000ten into 32-bit two’s complement binary numbers,
respectively, and convert the following two’s complement binary numbers to be
decimal numbers:
a.
1111 1111 1111 1111 1111 1110 0000 1100two;
b.
1111 1111 1111 1111 1111 1111 1111 1111two;
c.
0111 1111 1111 1111 1111 1111 1111 1111two.
2.
The following MIPS instruction sequence
could be used to implement a new instruction that has two register operands.
Give the instruction a name and describe what it does. Note that register $t0
is being used as a temporary.
srl $s1, $s1, 1 #
sll $t0, $s0, 31 #
These 4 instructions accomplish “new $s0 $s1”
srl $s0, $s0, 1 #
or $s1, $s1, $t0 #
3.
The ALU supported set on less than (slt)
using just the sign bit of the adder. Let’s try a set on less than operation
using the values -7ten and 6ten. To make it simpler to
follow the example, let’s limit the binary representations to 4 bits: 1001two
and 0110two.
1001two
– 0110two = 1001two + 1010two = 0011two
This result
would suggest that -7ten > 6ten, which is clearly
wrong. Hence we must factor in overflow in the decision. Modify the 1-bit ALU
in the following figures to handle slt correctly.
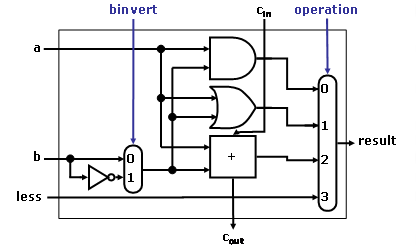
Figure 1: A 1-bit ALU that performs AND, OR, and addition on a and
b or b’.

Figure 2: A 1-bit ALU for the most significant bit.
4.
Show the IEEE 754 binary representation
for the floating-point number 10ten, 10.5ten, 0.1ten,
and -2/3, respectively.