Computer Organization and Structure
Homework #3
Due: 2004/11/9
1.
Convert 4096ten, -2,047ten,
and -2,000,000ten into 32-bit two’s complement binary numbers,
respectively, and convert the following two’s complement binary numbers to be
decimal numbers:
a.
1111 1111 1111 1111 1111
1111 0000 0110two;
b.
1111 1111 1111 1111 1111
1111 1110 1111two;
c.
0111 1111 1111 1111 1111 1111
1110 1111two.
2.
Suppose that all of the conditional branch
instructions except beq and bne were removed
from the MIPS instruction set along with slt and all of
its variants (slti, sltu, sltui). Show how
to perform
slt $t0, $s0, $s1
using the modified
instruction set in which slt is not
available. (Hint: It requires more than two instructions.)
3.
The ALU supported set on less than (slt) using just
the sign bit of the adder. Let’s try a set on less than operation using the
values -7ten and 6ten. To make it simpler to follow the
example, let’s limit the binary representations to 4 bits: 1001two
and 0110two.
1001two
– 0110two = 1001two + 1010two = 0011two
This result
would suggest that -7ten > 6ten, which is clearly
wrong. Hence we must factor in overflow in the decision. Modify the 1-bit ALU
in the following figures to handle slt correctly.
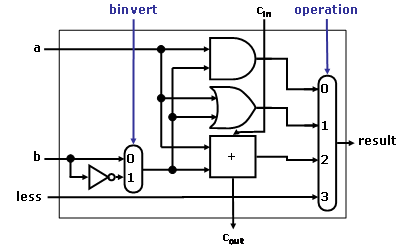
Figure 1: A 1-bit ALU that performs AND, OR, and addition on a and b or b’.
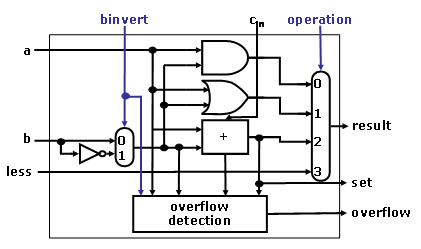
Figure 2: A 1-bit ALU for the most significant bit.
4.
Add 2.85ten x 103 to 9.84ten
x 104 and add 3.63ten x 104 to 6.87ten
x 103, respectively, assuming that you have only three significant
digits, first with guard and round digits and then without them.
5.
Show the IEEE 754 binary representation for the
floating-point numbers 20ten, 20.5ten, 0.1ten,
and -5/6, respectively.