Computer Organization and Structure
Homework
#2
Due:
2008/10/28
Please
write the following three programs in MIPS assembly language.
1.
Triangle
Determination (30%):
We
will give you three positive numbers as the length for each straight line
segment, and your job is to write a program to determine whether these three
line segments can form a triangle or not.
Your output should
look like this.
----Triangle Determination---
Please type 3 integers, and each with the
Enter keys.
N1
N2
N3
Length N1, N2, N3 line segments [CAN /
CANNOT] form a triangle.
2. Variation of Fibonacci sequence (35%):
We
all understand the well-known Fibonacci sequence which is defined by the
following recurrence relation.
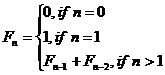 …Def. A
…Def. A
Now we make some
variations on the original
Fibonacci numbers with the new definition as following.
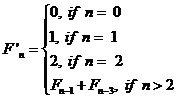 …Def. B
…Def. B
In
order to let you students get more understanding of how to use assembly
language to implement recursive call, you are asked to write a program which
computes the modified Fibonacci numbers as Def. B defined.
Your
output should look like this
----Variation of Fibonacci ---
Please type 1 integer, and then press
Enter keys.
13
The result of F’13 is 101
3. Prime number finding
(35%):
Your
third task is to write a program to find the largest prime number which is
smaller than or equal to a user-defined number. You should read in a positive
number n from the console, then find
and display the largest prime number which is also smaller than n. For example, if user input is a
positive number 30, and your function should find out the largest prime number
within the range [0, 30], which is 23.
Here
we introduce the Sieve of Eratosthenes algorithm to solve this problem. The
most efficient way to find all of the small primes (say all those less than
10,000,000) is by using the Sieve of Eratosthenes (ca 240 BC):
For
example, to find all the primes less than or equal to 30, first list the
numbers from 2 to 30.
2 3 4
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
The
first number 2 is prime, so keep it (we will color it green) and cross out its
multiples (we will color them red), so the red numbers are not prime.
2
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
The
first number left (still black) is 3, so it is the first odd prime. Keep it and
cross out all of its multiples. We know that all multiples less than 9 (i.e. 6)
will already have been crossed out, so we can start crossing out at 32=9.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Now
the first number left (still black) is 5, the second odd prime. So keep it also
and cross out all of its multiples (all multiples less than 52=25
have already been crossed out, and in fact 25 is the only multiple not yet
crossed out).
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
The
next number left, 7, is larger than the square root of 30, so there are no
multiples of 7 to cross off that haven't already been crossed off (14 and 28 by
2, and 21 by 3), and therefore the sieve is complete. Therefore all of the
numbers left are primes: {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}. Notice we just
found these primes without dividing.
This
algorithm can be written in c++ as follows
unsigned int Eratosthenes(unsigned int n) {
unsigned
int Sieve[500];
Sieve[0]
= Sieve[1] = 0;
for(unsigned
int i = 2 ; i < 500; i++)
Sieve[i]
= 1;
for
(unsigned int i = 2; i * i < 500; i++)
if
(Sieve[i] == 1)
for
(unsigned int j = (i + i); j < 500; j += i)
Sieve[j]
= 0;
for
(unsigned int j = 499; j > 1; j--)
if
(Sieve[j] == 1)
return
j;
return
0;
}
In
the final testing, we will use the number which is smaller than 500 as n.
Your
output should look like this.
----Finding Largest Prime Function---
Please type 1 integer which is between 2
and 500, and then press Enter keys.
445
The largest prime between 2 and 445 is
443.
Submission
& Grading
|
Description |
For Each Problem |
|
Program runs
without error message |
10% |
|
Program executes
correctly |
60% |
|
Documentation
and description of the program |
10% |
|
Presentation |
10% |
|
Implement Detail |
10% |